The AI Superhighway: How Manifold-Constrained Hyper-Connections (mHC) Prevent Traffic Jams in Large Language Models by DeepSeek

🤖 Taming the AI Titans: The Secret to Scaling Giant Models

DeepSeek: mHC: Manifold-Constrained Hyper-Connections
https://arxiv.org/pdf/2512.24880
Zhenda Xie*†, Yixuan Wei*, Huanqi Cao*, Chenggang Zhao, Chengqi Deng, Jiashi Li, Damai Dai, Huazuo Gao, Jiang Chang, Liang Zhao, Shangyan Zhou, Zhean Xu, Zhengyan Zhang, Wangding Zeng, Shengding Hu, Yuqing Wang, Jingyang Yuan, Lean Wang, Wenfeng Liang

1. The Bottleneck on AI's Information Highway

For nearly a decade, a simple but powerful architectural feature has been the backbone of deep learning models like the Transformers that power today's Large Language Models (LLMs). This feature is the residual connection.

You can think of a standard residual connection as a single-lane highway. It provides a direct, uninterrupted path for information (the traffic) to travel from the beginning of a deep network to the end, bypassing the complex processing happening in each layer (the city streets).

This direct path creates what's known as an identity mapping. Its purpose is elegantly simple: it ensures that the core signal from early layers can reach later layers without getting lost or distorted. Just as a straight highway prevents cars from getting lost on winding city roads, the identity mapping provides a stable path that prevents training from collapsing, especially in very deep models.

However, as AI models have grown exponentially larger and deeper, this reliable single-lane highway has become a major bottleneck. The model's computational blocks—the city streets—are becoming more powerful and complex, capable of incredible feats. But they are all being fed by the same single-lane highway, starving them of the rich, multi-faceted information they are now built to process.

This bottleneck presented a fundamental challenge and led researchers to explore a new way to widen the road.

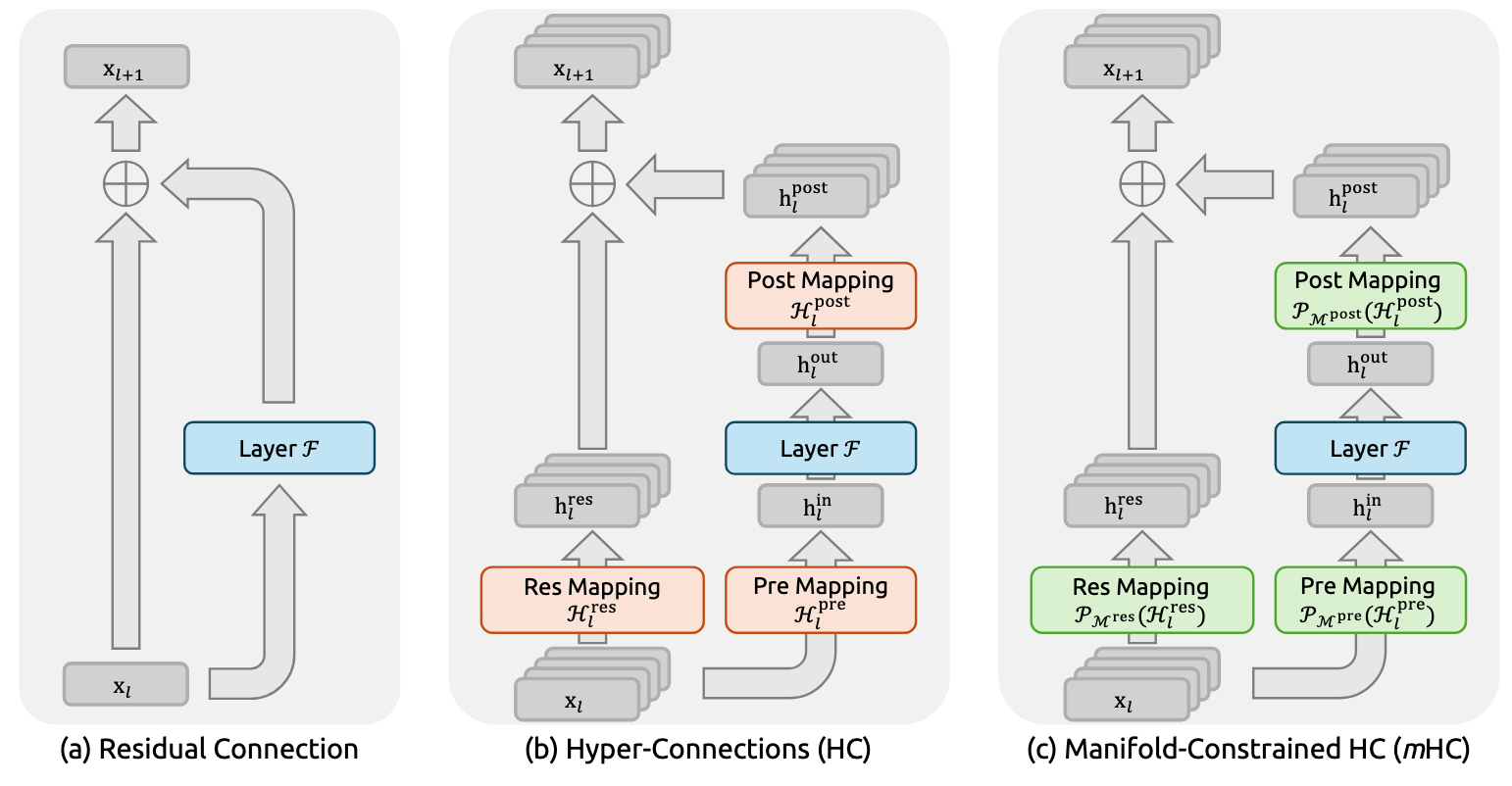
2. A Wider Highway with a Fatal Flaw: Hyper-Connections (HC)

The first logical step to solve the bottleneck was to widen the information highway. This is the core idea behind Hyper-Connections (HC). Instead of a single stream of information, HC expands the residual connection into multiple parallel streams—for example, four—creating a multi-lane superhighway. This dramatically increases the "information bandwidth" with almost no extra computational cost (FLOPs).

But this wider highway came with a fatal flaw. To allow the parallel streams to share information, HC replaced the stable, passive "identity mapping" with unconstrained, learnable mixing matrices. And this is where the system broke down.

Imagine installing faulty, experimental turbochargers in every car at every toll booth along this new superhighway. At the first booth, each car gets a small, seemingly harmless boost. But at the next booth, that already-boosted speed is amplified again, and again at the next. Very quickly, this compounding effect causes the cars to accelerate uncontrollably until they careen off the road in a catastrophic crash.

This is precisely what happens inside a deep network with unconstrained Hyper-Connections. The learnable matrices cause "unbounded signal amplification" because the core issue is the composite mapping created by multiplying these matrices layer after layer. A single matrix with a spectral norm of 1.05 might seem harmless. But sixty of them multiplied together? That’s 1.05⁶⁰, resulting in an 18.7x amplification. The "crash" manifests as severe training instability and a sudden loss surge, where the model's error rate unexpectedly skyrockets.

Empirical evidence confirmed this structural failure. In a 27B parameter model, this instability caused signal gains to exceed 3000x, leading to a catastrophic training divergence. Data from the model's training run showed a sudden, unexpected spike in the loss curve, which correlated perfectly with extreme values in signal amplification.

The challenge, then, was clear: How can we get the benefits of a multi-lane highway without the catastrophic crashes?

3. The Elegant Solution: Manifold-Constrained Hyper-Connections (mHC)

The solution is Manifold-Constrained Hyper-Connections (mHC), an approach that keeps the multi-lane superhighway but imposes a simple, powerful set of "rules of the road" to ensure every vehicle stays safely in its lane and travels at a controlled speed.

3.1 The Golden Rule: Doubly Stochastic Matrices

The core of mHC is a mathematical constraint: the mixing matrices are forced to be doubly stochastic. This sounds complex, but the rules are straightforward and intuitive.

• All entries are non-negative. The matrix cannot subtract or cancel out information.
• All rows must sum to 1. This controls how information is distributed out from each stream.
• All columns must also sum to 1. This controls how information is received in by each stream.

The best way to understand this is through a geometric interpretation. A doubly stochastic matrix is essentially a weighted average of permutations.

First, a simple permutation matrix just shuffles information. It can reorder the streams, but it cannot amplify or diminish the total signal. It's a pure rearrangement.

A doubly stochastic matrix takes this a step further: it acts as a convex combination—a balanced, weighted average—of these shuffles. This allows for rich mixing between streams, but because it's just an average of shuffles, it is mathematically guaranteed not to amplify the signal. It's a mixing mechanism, not an amplifier.

This simple constraint transforms the connection from a source of instability into a stable and balanced information-mixing mechanism.

3.2 The Three Guarantees of Stability

By enforcing this rule, mHC provides three powerful, mathematically guaranteed properties that are essential for training massive AI models.

1. Guaranteed Norm Preservation This property acts like a universal speed limit. It makes it structurally impossible for the signal to explode, no matter how many layers it passes through.
2. Depth-Independent Stability The set of doubly stochastic matrices is "closed under matrix multiplication," meaning that if you multiply two such matrices together, the result is also a doubly stochastic matrix. This is the key insight: it means that no matter how many layers you stack, the composite mapping that governs the signal flow from the first to the last layer also remains doubly stochastic. Stability is guaranteed for the entire network, not just one step.
3. Balanced Information Mixing This constraint turns the connection into a robust feature fusion mechanism. Instead of uncontrollably amplifying signals, it fairly shuffles and combines information from all streams, allowing for rich representations without sacrificing stability.

With this elegant theory in place, the next step was to prove its effectiveness in the real world.

4. The Proof: mHC in Action

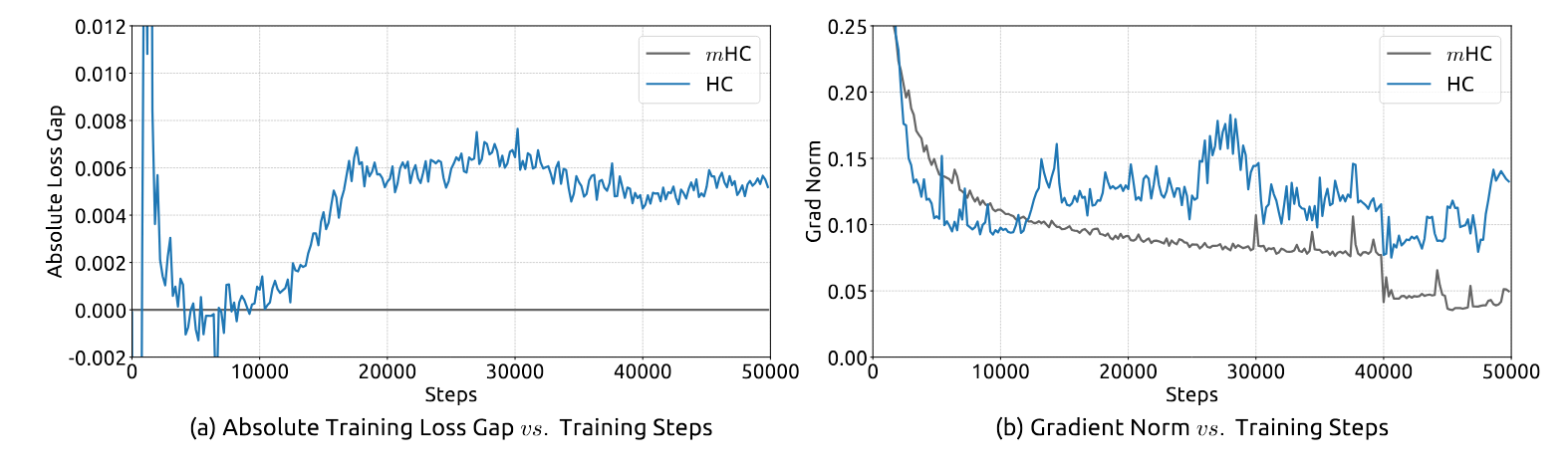
4.1 Taming the Signal Explosion

When put to the test, mHC performed exactly as the theory predicted, completely eliminating the instability that plagued the unconstrained HC approach. The data shows a night-and-day difference in stability.

4.2 Achieving Superior Performance

Crucially, mHC doesn't just fix instability—it unlocks superior performance. This newfound stability wasn't just for safety—it unlocked a new level of performance. By enabling a wider, more expressive information flow, it allows the model to learn more effectively.

These results show that by solving the stability problem, mHC allows the architectural benefits of wider residual streams to be fully realized.

5. From Theory to Reality: Making mHC Efficient

The mathematical elegance of mHC would be useless if it were too slow or memory-intensive for real-world training. Widening the information highway from one lane to four inevitably increases memory traffic, which can create a "memory wall" that slows down the GPU. To make mHC practical, a series of clever engineering optimizations were required.

• Kernel Fusion: Combining multiple GPU operations into one to reduce the "memory wall" bottleneck. This is like making one big trip to the grocery store for all your ingredients instead of ten separate trips, saving time and energy.
• Selective Recomputation: Saving GPU memory by discarding some intermediate results and recalculating them later. This is like throwing away your scratch paper after solving a math problem to save desk space, knowing you can easily recalculate the intermediate steps if you need to check your work.
• DualPipe Overlapping: Hiding communication latency by having the GPU compute and send data at the same time. This is like a chef starting to prep the next course while the current one is still cooking, ensuring the kitchen never sits idle.

The Bottom Line: These optimizations are so effective that they allow a 4x wider residual stream to be implemented with only a 6.7% additional training time overhead. This is the critical step that makes mHC a practical tool, not just a theoretical curiosity.

6. Conclusion: The New Blueprint for Scaling AI

The development of Manifold-Constrained Hyper-Connections is more than just an incremental tweak. It represents a fundamental shift in how we build and scale the next generation of AI models. For years, the approach to instability has been to penalize it with techniques like gradient clipping or regularization. The core insight of mHC is to move from fixing instability to preventing it with structural constraints. By constraining the mixing matrices to the manifold of doubly stochastic matrices, mHC makes signal explosion structurally impossible, not just penalized. It redesigns the geometry of the solution space itself.

This breakthrough proves that stability and expressiveness do not have to be a trade-off. The success of mHC stands on three pillars: the mathematical rigor of Manifold Theory, the architectural insights of Transformer Architecture, and the practical execution of GPU Systems Engineering. The intelligent integration of these three disciplines provides a powerful new blueprint for building foundational models that are more stable, scalable, and ultimately, more capable than ever before.